C Program to Calculate area of right angle triangle

Introduction

Welcome to our comprehensive guide on calculating the area of a right-angled triangle. In this article, we will provide you with a step-by-step approach to accurately determine the area of a right-angled triangle. By following the methods outlined below, you will gain a solid understanding of this calculation and be able to apply it effectively in various scenarios.

Understanding Right-Angled Triangles

A right-angled triangle is a polygon with three sides, where one angle measures exactly 90 degrees, forming a perfect right angle. It is essential to familiarize yourself with the different components of a right-angled triangle before proceeding with the area calculation.

Components of a Right-Angled Triangle

1. Hypotenuse (H): The side opposite the right angle is known as the hypotenuse. It is denoted by the letter “H” and is the longest side of the triangle.
2. Legs (L1 and L2): The other two sides of the right-angled triangle are called legs. They are denoted by “L1” and “L2”.

To calculate the area of a right-angled triangle, we will utilize a simple formula based on the lengths of its legs.

The Area Formula

The formula to calculate the area of a right-angled triangle is as follows:

Area = (L1 * L2) / 2

To obtain the area, multiply the lengths of the two legs and divide the result by 2. This formula holds true for any right-angled triangle, regardless of the specific measurements of its legs.

Step-by-Step Calculation

To demonstrate the calculation process, let’s consider an example with specific leg measurements:

• Leg 1 (L1) = 5 units
• Leg 2 (L2) = 8 units

Now, let’s calculate the area using the formula we mentioned earlier:

Area = (5 * 8) / 2
     = 40 / 2
     = 20 square units

Therefore, for a right-angled triangle with legs measuring 5 units and 8 units, the area is 20 square units.

Importance of Calculating the Area of a Right-Angled Triangle

The area of a right-angled triangle plays a significant role in various fields, including geometry, engineering, architecture, and construction. By accurately determining the area, professionals in these disciplines can make precise calculations and design plans accordingly.

C Program to Calculate area of right angle triangle

#include<stdio.h>
int main()
{
    double base,height,area;
    printf("Enter base and height : ");
    scanf("%lf %lf",&base,&height);
    area=.5*base*height ;
    printf("Area of right triangle is:%.3lf",area);
    return 0;


}

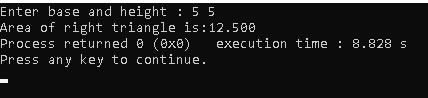
Output:

Conclusion

In conclusion, calculating the area of a right-angled triangle is a fundamental mathematical operation with practical applications in various domains. By following the step-by-step approach outlined in this guide, you can confidently determine the area of any right-angled triangle you encounter. Remember to use the formula (L1 * L2) / 2, where L1 and L2 represent the lengths of the triangle’s legs. By mastering this calculation, you will enhance your problem-solving abilities and gain a deeper.

read more

Example 5. Area of the rectangle in C